|
11560 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
 Kansrekenen
KansrekenenKansrekenen (of kansberekenen) is een tak van de wiskunde die zich bezighoudt met toevalssituaties: hoe groot is de kans dat iets gebeurt? Daar zijn vaak ingewikkelde modellen en formules voor, die we niet allemaal zullen behandelen bij Beter Rekenen. Maar eenvoudige kansberekeningen komen soms wel aan bod in een opgave. Een paar voorbeelden:

Dobbelstenen
Hoe groot is de kans dat je 4 gooit met 1 gewone dobbelsteen?
- Een dobbelsteen heeft 6 kanten. Als het een normale, eerlijke dobbelsteen is en je gooit 36 keer, gooi je elk cijfer ongeveer 6 keer. Je gooit 4 bij gemiddeld is 1 op de 6 worpen.
- De kans dat je 4 gooit is 1 op 6.
- Het is een kans van 1 : 6 (spreek uit als: '1 op 6').
Hoe groot is de kans dat je met 1 dobbelsteen hoger dan 2 gooit?
- Van de 6 mogelijke cijfers zijn er vier hoger dan 2 (namelijk 3, 4, 5 en 6).
- De kans dat je hoger dan 2 gooit, is een kans van 4 : 6.
- Dat mag je vereenvoudigen, zoals bij breuken. Het is een kans van 2 : 3.
Nu met twee dobbelstenen: hoe groot is de kans dat je twee vieren tegelijk gooit?
- Bekijk de dobbelstenen een voor een.
- Voor de eerste dobbelsteen is de kans 1 : 6.
- De kans dat de tweede dobbelsteen ook een 4 wordt, is ook 1 : 6.
- Je kunt deze kansen met elkaar vermenigvuldigen alsof het twee breuken zijn:
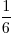 x
x 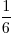 =
= 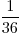
- De kans op twee vieren is 1 : 36.
Gemiddeld genomen heb je 36 worpen nodig om een keer twee vieren te gooien.
Nog eens twee dobbelstenen: hoe groot is de kans dat je twee gelijke cijfers gooit?
- Bekijk de dobbelstenen een voor een.
- Voor de eerste dobbelsteen maakt het nog niet uit. Deze bepaalt wat de waarde van de tweede dobbelsteen moet zijn om twee gelijke cijfers te gooien.
- Voor de tweede dobbelsteen geldt een kans van 1 : 6 dat deze hetzelfde is als de eerste.
- De kans op twee gelijke cijfers is 1 : 6.
Nog eens twee dobbelstenen: hoe groot is de kans dat je twee verschillende cijfers gooit?
- Bekijk de dobbelstenen een voor een.
- Voor de eerste dobbelsteen maakt het nog niet uit. Deze bepaalt wat de waarde van de tweede dobbelsteen niet mag zijn om twee verschillende cijfers te gooien.
- Voor de tweede dobbelsteen geldt een kans van 5 : 6 dat deze anders is dan de eerste.
- De kans op twee verschillende cijfers is 5 : 6.
Nog eens twee dobbelstenen: hoe groot is de kans dat je een 2 en een 3 gooit?
- Bekijk de dobbelstenen een voor een.
- De eerste dobbelsteen mag 2 of 3 zijn. Dat is een kans van 2 : 6, oftewel een kans van 1 : 3.
- De tweede dobbelsteen moet nu het andere cijfer zijn. Als de eerste dobbelsteen 2 is, moet de tweede dobbelsteen 3 zijn en andersom. De tweede dobbelsteen moet precies die ene waarde hebben die je nog mist. Daarvoor geldt een kans van 1 : 6.
- Je kunt nu deze twee kansen met elkaar vermenigvuldigen, zoals je dat ook zou doen met breuken:
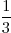 x
x 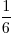 =
= 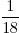 . Het is een kans van 1 : 18.
. Het is een kans van 1 : 18. - Dat klopt, want van de 36 worpen (1-1, 1-2, 1-3, enzovoort t/m 6-6) voldoen er twee aan de voorwaarde: 2-3 en 3-2. Een kans van 2 : 36 is hetzelfde als 1 : 18.
Nu met drie dobbelstenen: hoe groot is de kans dat je twee zessen en één vijf gooit?
- Bekijk de dobbelstenen een voor een.
- Als je 6-6-5 wilt gooien, moet de eerste dobbelsteen een 6 zijn. Dat is een kans van 1 : 6. De tweede dobbelsteen moet ook een 6 zijn (weer een kans van 1 : 6) en de derde moet een 5 zijn (ook een kans van 1 : 6). Dat zou een kans van 1 : 216 zijn.
- Maar je gooit de dobbelstenen tegelijk. Het mag daarom ook 6-5-6 of 5-6-6 zijn.
- Er zijn drie combinaties mogelijk met één vijf en twee zessen. In de wiskunde noemen ze die verschillende mogelijkheden 'permutaties'.
- De kans is 3 : 216.
- Dat is een kans van 1 : 72.
Tot zover de dobbelstenen. Door op bovenstaande manier te redeneren, kun je heel veel kansberekeningen oplossen.
Knikkers
Je hebt een bak met 5 rode, 4 blauwe en 3 gele knikkers. Totaal 12 knikkers.
Je pakt willekeurig 1 knikker.
- De kans op een rode knikker is 5 : 12.
- De kans op een blauwe knikker is 4 : 12, oftewel 1 : 3.
- De kans op een gele knikker is 3 : 12, oftewel 1 : 4.
Je pakt twee knikkers uit de genoemde bak. Hoe groot is de kans dat het twee gele knikkers zijn?
- De kans dat de eerste knikker geel is, is 1 : 4.
- Daarna zijn er nog 2 gele knikkers in een bak van 11 knikkers. De kans dat de tweede knikker geel is, is 2 : 11.
- Je kunt de kansen (1 : 4) en (2 : 11) met elkaar vermenigvuldigen, alsof het twee breuken zijn.
- De kans dat je twee gele knikkers pakt, is 2 : 44, oftewel 1 : 22.
Je pakt twee knikkers uit de genoemde bak. Hoe groot is de kans dat deze dezelfde kleur hebben?
- De kans op twee gele knikkers is 1 : 22.
- Op dezelfde manier kun je uitrekenen wat de kans op twee blauwe knikkers is:
(1 : 3) x (3 : 11) = 3 : 33 = 1 : 11 - Op dezelfde manier kun je uitrekenen wat de kans op twee rode knikkers is:
(5 : 12) x (4 : 11) = 20 : 132 = 5 : 33. - Nu moet je drie verhoudingen bij elkaar optellen. De kans dat je twee dezelfde kleuren pakt is:
(1 : 22) + (1 : 11) + (5 : 33). - Behandel dit als breuken die je eerst gelijknamig moet maken:
(3 : 66) + (6 : 66) + (10 : 66) = 19 : 66.
Kans uitdrukken in procenten
Vaak wordt een kans uitgedrukt in procenten. Het omrekenen naar procenten is eigenlijk hetzelfde als het omrekenen van breuken naar kommagetallen en procenten.
Een aantal van de kansen die hierboven genoemd worden, zijn:
- een kans van 1 : 2 is een kans van 50%.
- een kans van 3 : 4 is een kans van 75%.
- een kans van 1 : 18 is een kans van 5,556% (afgerond)
- een kans van 1 : 22 is een kans van 4,545% (afgerond)
- een kans van 19 : 66 is een kans van 28,788% (afgerond)
Opmerking tot slot: het is kansberekening.
Uitkomsten blijven onvoorspelbaar. Als je zes keer met een dobbelsteen gooit, is niet precies 1 van die worpen een 4. Statistisch, gemiddeld over heel veel worpen klopt het wel, maar het is nog steeds mogelijk om 6 keer achtereen een 4 te gooien, hoe onwaarschijnlijk dat ook is.
© 2010 - Beter Rekenen is een initiatief van |
