|
11560 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
 Machtsverheffen
MachtsverheffenMachtsverheffen is herhaald vermenigvuldigen.
Kwadraat
Het bekendste voorbeeld van machtsverheffen is het kwadraat, bijvoorbeeld 42 (spreek uit: vier kwadraat).
42 = 4 x 4 = 16
122 = 12 x 12 = 144
Hier volgt een overzicht van kwadraten t/m 1002 (dan hoef je die niet meer uit te rekenen):
| 1 | 1 | 26 | 676 | 51 | 2601 | 76 | 5776 | |||
| 2 | 4 | 27 | 729 | 52 | 2704 | 77 | 5929 | |||
| 3 | 9 | 28 | 784 | 53 | 2809 | 78 | 6084 | |||
| 4 | 16 | 29 | 841 | 54 | 2916 | 79 | 6241 | |||
| 5 | 25 | 30 | 900 | 55 | 3025 | 80 | 6400 | |||
| 6 | 36 | 31 | 961 | 56 | 3136 | 81 | 6561 | |||
| 7 | 49 | 32 | 1024 | 57 | 3249 | 82 | 6724 | |||
| 8 | 64 | 33 | 1089 | 58 | 3364 | 83 | 6889 | |||
| 9 | 81 | 34 | 1156 | 59 | 3481 | 84 | 7056 | |||
| 10 | 100 | 35 | 1225 | 60 | 3600 | 85 | 7225 | |||
| 11 | 121 | 36 | 1296 | 61 | 3721 | 86 | 7396 | |||
| 12 | 144 | 37 | 1369 | 62 | 3844 | 87 | 7569 | |||
| 13 | 169 | 38 | 1444 | 63 | 3969 | 88 | 7744 | |||
| 14 | 196 | 39 | 1521 | 64 | 4096 | 89 | 7921 | |||
| 15 | 225 | 40 | 1600 | 65 | 4225 | 90 | 8100 | |||
| 16 | 256 | 41 | 1681 | 66 | 4356 | 91 | 8281 | |||
| 17 | 289 | 42 | 1764 | 67 | 4489 | 92 | 8464 | |||
| 18 | 324 | 43 | 1849 | 68 | 4624 | 93 | 8649 | |||
| 19 | 361 | 44 | 1936 | 69 | 4761 | 94 | 8836 | |||
| 20 | 400 | 45 | 2025 | 70 | 4900 | 95 | 9025 | |||
| 21 | 441 | 46 | 2116 | 71 | 5041 | 96 | 9216 | |||
| 22 | 484 | 47 | 2209 | 72 | 5184 | 97 | 9409 | |||
| 23 | 529 | 48 | 2304 | 73 | 5329 | 98 | 9604 | |||
| 24 | 576 | 49 | 2401 | 74 | 5476 | 99 | 9801 | |||
| 25 | 625 | 50 | 2500 | 75 | 5625 | 100 | 10000 |
Het verschil tussen kwadraten
Voor het uitrekenen van het verschil tussen twee kwadraten, kun je ook deze formule gebruiken:
- a2 - b2 = (a + b) x (a - b)
Bijvoorbeeld:
162 - 122 = (16 + 12) x (16 - 12) = 28 x 4 = 112
Dat rekent misschien sneller dan:
162 - 122 = 256 - 144 = 112
zie ook de pagina Merkwaardige producten.
Exponent groter dan 2
Het kleine hoger geschreven getal wordt exponent genoemd.
Als de exponent groter wordt, wordt de vermenigvuldiging vaker herhaald, bijvoorbeeld 23 (uitgesproken als: "twee tot de derde" of "twee tot de derde macht" of "twee tot de macht drie").
23 = 2 x 2 x 2 = 8
43 = 4 x 4 x 4 = 64
210 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1024
Bij Beter Rekenen zullen we op niveau 3F af en toe iets doen met machtsverheffen, maar hoofdzakelijk met een exponent van 2 of 3.
Exponent 1
De exponent is dus het aantal keren dat je het getal wordt vermenigvuldigd.
Iets tot de eerste macht, kan dat ook? Ja, dat bestaat ook.
Kijk eens naar de volgende regelmaat:
33 = 3 x 3 x 3 = 27
32 = 3 x 3 = 9
31 = ..............?
Telkens als de exponent 1 kleiner wordt, wordt de uitkomst in bovenstaand voorbeeld gedeeld door 3.
De laatste stap, van 32 naar 31 is dan ook weer een deling door 3. Die levert het getal 3 als uitkomst op. Dus:
31 = 9 : 3 = 3
Exponent 0
En hoe zit dat dan met "iets tot de macht nul"?
33 = 27
32 = 9
31 = 3
30 = ..............?
Als de exponent 1 kleiner wordt, wordt de uitkomst in bovenstaand voorbeeld gedeeld door 3.
De stap van 31 naar 30 is ook weer een deling door 3. Die levert het getal 1 als uitkomst op.
30 = 1
Dit geldt ook voor elk ander positief getal:
10 = 1
20 = 1
30 = 1
40 = 1
8750 = 1
Negatieve exponent
En als je voortborduurt op bovenstaand rijtje, kun je ook beredeneren wat 3(-1) en 3(-2) zal betekenen.
33 = 3 x 3 x 3 = 27
32 = 3 x 3 = 9
31 = 3 = 3
30 = 1
3-1 = 1 : 3 = 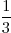
3-2 = 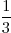 : 3 =
: 3 = 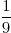
3-3 = 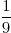 : 3 =
: 3 = 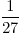
© 2010 - Beter Rekenen is een initiatief van |
