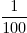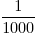Antwoorden van 21-01-2026 (niveau 3F)
21 JAN 
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 21-01-2026 zo ingevuld:
Welk getal ligt precies in het midden tussen -4,8 en -1,6?
-3,2 
-3,3-3,6-2,6Tel eerst -4,8 en -1,6 bij elkaar op en deel het resultaat door 2. Dus -4,8 + -1,6 = -6,4 en -6,4 : 2 = -3,2
Of met een getallenlijn:
Op een getallenlijn is de afstand tussen beide getallen 3,2. De helft is 1,6. Het gevraagde getal ligt op de getallenlijn 1,6 rechts van -4,8 en ook 1,6 links van -1,6. In beide gevallen -3,2.
Zie ook de pagina Gemiddelde.
Of met een getallenlijn:
Op een getallenlijn is de afstand tussen beide getallen 3,2. De helft is 1,6. Het gevraagde getal ligt op de getallenlijn 1,6 rechts van -4,8 en ook 1,6 links van -1,6. In beide gevallen -3,2.
Zie ook de pagina Gemiddelde.
deel is hetzelfde als0,005%0,0005%0,5%0,05% 
Het etiket van een fles limonadesiroop zegt dat de limonade op z'n lekkerst is als 5% van de vloeistof uit limonadesiroop bestaat. Er zit nog 25 mL siroop in de fles. Hoeveel limonade kun je dan maken met deze hoeveelheid volgens dit recept?
0,5 liter 0,05 liter50 dL0,5 cL
Kijk eerst naar het plaatje hierboven. Beide wippen zijn in balans. In het eerste geval hebben ze beide 10 kg op 2 meter vanaf het scharnierpunt. In het tweede geval is het rechter gewicht 20 kg op 1 meter vanaf het scharnierpunt (het gewicht is verdubbeld en de afstand gehalveerd).
Onderstaand sommetje gaat over deze eigenschap van zo'n wip.
Vader Gerard en dochters Dianne en Mieke wandelen in het bos. Ze zien een boomstam dwars over een andere liggen. Ze besluiten die als wipwap te gebruiken.
Gerard (90 kg) gaat op 1 meter van het scharnierpunt zitten. Als Dianne en Mieke (elk 30 kg) op respectievelijk 1 en 2 meter vanaf het scharnierpunt tegenover hem zitten komt de wipwap in evenwicht.
Gerard schuift 20 cm dichterbij en gaat daardoor omhoog. Hoeveel cm moet Dianne dichterbij schuiven om de wipwap weer in evenwicht te krijgen?
20 cm30 cm40 cm60 cm (Een som van Estee.)
Gewicht x afstand aan beide kanten moet gelijk zijn.
Bovenste plaatje:
(90 x 1) = (30 x 1) + (30 x 2)
Nieuwe toestand (90 x 0.8) = (30 x 0.4) + (30 x 2)
Je kunt het ook anders beredeneren:
Het gewicht van Gerard (90 kg) schuift 20 cm naar het scharnierpunt. Aan de andere kant moet dat gecompenseerd worden met het verschuiven van 30 kg dat even ver van het scharnierpunt af zit. 30 kg is 1/3 van 90 kg. Voor een evengroot effect moet dat kleinere gewicht 3x zo ver opschuiven.
3 x 20 cm = 60 cm.
Zie ook de pagina Verhoudingen.
Gewicht x afstand aan beide kanten moet gelijk zijn.
Bovenste plaatje:
(90 x 1) = (30 x 1) + (30 x 2)
Nieuwe toestand (90 x 0.8) = (30 x 0.4) + (30 x 2)
Je kunt het ook anders beredeneren:
Het gewicht van Gerard (90 kg) schuift 20 cm naar het scharnierpunt. Aan de andere kant moet dat gecompenseerd worden met het verschuiven van 30 kg dat even ver van het scharnierpunt af zit. 30 kg is 1/3 van 90 kg. Voor een evengroot effect moet dat kleinere gewicht 3x zo ver opschuiven.
3 x 20 cm = 60 cm.
Zie ook de pagina Verhoudingen.
TOTAALRESULTAAT:
71% goedUitleg van de kleuren en symbolen:
het juiste antwoord (door jou gekozen)
een fout antwoord (door jou gekozen)Help | Contact | Instellingen |
Martin van Toll Producties