|
0 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
 |
|
|
|
Dit is een muismat van Beter Rekenen:
Breuken, kommagetallen en procenten.
Een spiekbrief onder je muis bestellen?
Kies uit vier modellen.
Antwoorden van 10-12-2025 (niveau 3F)
10 DEC 
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 10-12-2025 zo ingevuld:
Computers werken met nullen en enen, binaire getallen. De binaire getallen 1, 10, 100 en 1000 zijn in het normale tientallig stelsel 1, 2, 4 en 8 (oftewel 2 tot de macht 0, 1, 2, en 3).
Je kunt binaire getallen omrekenen naar "normale", decimale getallen.
0 = 0,
1 = 1,
10 = 2,
11 = 3,
100 = 4,
101 = 5, enzovoort.
De decimale waarde van het binaire getal 11101 is ........ .
29 
andersBegin bij het achterste cijfer. Van rechts naar links staan de enen in het binaire getal voor decimale waarden 1, 2, 4, 8, enzovoort.
Van achter naar voren zijn de enen in 11101 waard: 1, 4, 8 en 16.
16 + 8 + 4 + 1 = 29
Zie ook de pagina Binaire getallen.
Van achter naar voren zijn de enen in 11101 waard: 1, 4, 8 en 16.
16 + 8 + 4 + 1 = 29
Zie ook de pagina Binaire getallen.
Hoeveel is 0,05% van 400?
2200,2 0,020,05% van 400 = 5% van 4
5% is hetzelfde als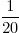
deel
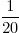van 4 = 0,2
Of:
5% van 400 is 20
0,5% is 2
0,05% is 0,2
Zie ook de pagina Makkelijke percentages.
5% is hetzelfde als
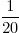deel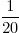 van 4 = 0,2Of:
5% van 400 is 20
0,5% is 2
0,05% is 0,2
Zie ook de pagina Makkelijke percentages.
Je hebt een kubus met een ribbe van 15 cm. Hoe lang zijn alle ribben samen?
90 cm180 cm 120 cm240 cmDe bovenkant heeft vier ribben, de onderkant ook en dan zijn er nog 4 staande ribben. Totaal 12 dus.
12 x 15 cm = 180 cm.
Zie ook de pagina Lengte.
12 x 15 cm = 180 cm.
Zie ook de pagina Lengte.
In de winkel liggen kaarsen met verschillende aantallen branduren:
1 kaars van 60 uren voor € 4,50.
1 kaars van 45 uren voor € 3,60.
2 kaarsen van elk 12 uren voor € 1,80 per set.
Een doos met 12 kaarsen van elk 3 uren voor € 2,52.
Als je let op de prijs per branduur is één soort het goedkoopst. Deze soort kost ........ cent per branduur.
(Vul het aantal centen in, geen euroteken. Indien nodig afronden.)
7 anders(Een som van Peter v.d. Zwaag.)
€ 4,50 : 60 = 7,5 cent
€ 3,60 : 45 = 8 cent
€ 1,80 : (2 x 12) = € 1,80 : 24 = 7,5 cent
€ 2,52 : (12 x 3) = € 2,52 : 36 = 7 cent
De doos van 12 stuks is dus per branduur het goedkoopst, namelijk 7 cent.
Zie ook de pagina Gemiddelde.
€ 4,50 : 60 = 7,5 cent
€ 3,60 : 45 = 8 cent
€ 1,80 : (2 x 12) = € 1,80 : 24 = 7,5 cent
€ 2,52 : (12 x 3) = € 2,52 : 36 = 7 cent
De doos van 12 stuks is dus per branduur het goedkoopst, namelijk 7 cent.
Zie ook de pagina Gemiddelde.
TOTAALRESULTAAT:
72% goedUitleg van de kleuren en symbolen:
het juiste antwoord (door jou gekozen)
een fout antwoord (door jou gekozen) 
Beter Spellen
Beter Rekenen
NU Beter Engels
NU Beter Duits
NU Beter Frans
NU Beter Spaans
Beter Bijbel
| © 2010 - Beter Rekenen is een initiatief van |