|
11293 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
Antwoorden van 02-03-2026 (niveau 3F)
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 02-03-2026 zo ingevuld:
4(2 + 7) = ........
Eerst uitrekenen wat tussen de haakjes staat en dan 4 x 9 = 36
Zie ook de pagina Gemengde bewerkingen.
Zie ook de pagina Gemengde bewerkingen.
3 van de 8 is hetzelfde als ...
Een regenton is precies voor
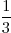 gevuld met water. Na een stevige onweersbui is de ton precies voor de helft gevuld. Er is tijdens de bui 12 liter water bij gekomen.
gevuld met water. Na een stevige onweersbui is de ton precies voor de helft gevuld. Er is tijdens de bui 12 liter water bij gekomen.Er kan in totaal ........ liter in deze regenton.
(Vul een geheel getal in.)
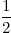 -
- 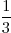 =
= 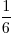
Er is tijdens de bui 12 liter water bij gekomen. Dat is
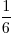 deel van de hele ton.
deel van de hele ton.De inhoud van de ton is 6 x 12 = 72 liter.
Zie ook de pagina Breuken aftrekken.
TOTAALRESULTAAT:
Uitleg van de kleuren en symbolen:
© 2010 - Beter Rekenen is een initiatief van |

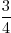 =
= 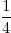
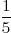
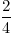 + 2
+ 2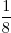 = 12,5%
= 12,5%