|
11067 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
Antwoorden van 17-07-2025 (niveau 3F)
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 17-07-2025 zo ingevuld:
De afstand tussen twee steden is 5500 km.
Op een kaart is de afstand 27,5 cm.
Op welke schaal is de kaart getekend?
27,5 cm op de kaart is in werkelijkheid 5500 km, oftewel 550.000.000 cm.
De verhouding is
27,5 : 550.000.000
Als je beide getallen door 27,5 deelt, zie je de schaal
1 : 20.000.000
Of:
Onthoud dat je te maken hebt met schaal
1 : 100.000 als 1 cm op de kaart 1 km in werkelijkheid is.
Bij schaal 1 : 100.000 zou 27,5 cm op de kaart 27,5 km in werkelijkheid zijn.
In de opgave is de werkelijkheid 200 keer zo groot, want
200 x 27,5 km = 5500 km.
De schaal is daarom
1 : 20.000.000
Zie ook de pagina Schaal.
De verhouding is
27,5 : 550.000.000
Als je beide getallen door 27,5 deelt, zie je de schaal
1 : 20.000.000
Of:
Onthoud dat je te maken hebt met schaal
1 : 100.000 als 1 cm op de kaart 1 km in werkelijkheid is.
Bij schaal 1 : 100.000 zou 27,5 cm op de kaart 27,5 km in werkelijkheid zijn.
In de opgave is de werkelijkheid 200 keer zo groot, want
200 x 27,5 km = 5500 km.
De schaal is daarom
1 : 20.000.000
Zie ook de pagina Schaal.
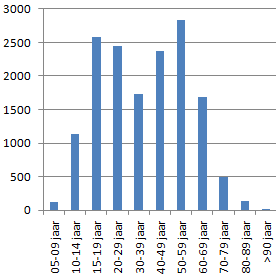
Ruim 15.000 deelnemers aan Beter Rekenen hebben bij hun profiel hun geboortejaar ingevuld. Het staafdiagram laat zien hoe de verschillende leeftijdsgroepen zijn verdeeld.
Het gaat hier om ongeveer 6000 mannen en 9000 vrouwen. Als deze verhouding in alle leeftijdsgroepen hetzelfde is, ongeveer hoeveel vrouwen van 60-69 jaar doen er dan mee?
("05-09 jaar" betekent "5 t/m 9 jaar")
40% mannen en 60% vrouwen.
60% van ongeveer 1700 = ongeveer 1020. Het antwoord 1000 komt het dichtst in de buurt.
Zie ook de pagina Diagrammen.
60% van ongeveer 1700 = ongeveer 1020. Het antwoord 1000 komt het dichtst in de buurt.
Zie ook de pagina Diagrammen.
Rond een boerderij lopen koeien, kippen, ganzen en eenden rond. Ze zijn allemaal gezond, op één kip na; die heeft slechts 1 poot. In totaal zijn er 125 dieren met in totaal 301 poten.
Er lopen ........ koeien op deze boerderij.
(Vul een geheel getal in)
(Een som van Jacques Schopman.)
Stel dat de gehandicapte kip 2 poten heeft. Dan zijn er in totaal 302 poten.
Elk van de dieren heeft dan 2 poten, behalve de koeien: die hebben er ieder 4.
Er zijn in totaal 125 dieren. Als dat allemaal tweepoters zijn, zijn er 250 poten. Je hebt nog 52 poten over. Daar kun je 26 koeien ieder nog 2 poten van toebedelen.
Of in een vergelijking met k voor het aantal koeien en t voor het aantal tweepoters (waarbij we voor het rekengemak de gehandicapte kip zijn tweede pootje teruggeven), kun je de volgende twee vergelijkingen maken:
4k + 2t = 302
k + t = 125
t = 125 - k
4k + 2(125 - k) = 302
4k + 250 - 2k = 302
2k = 302 -250 = 52
k = 26
Zie ook de pagina Vergelijkingen.
Stel dat de gehandicapte kip 2 poten heeft. Dan zijn er in totaal 302 poten.
Elk van de dieren heeft dan 2 poten, behalve de koeien: die hebben er ieder 4.
Er zijn in totaal 125 dieren. Als dat allemaal tweepoters zijn, zijn er 250 poten. Je hebt nog 52 poten over. Daar kun je 26 koeien ieder nog 2 poten van toebedelen.
Of in een vergelijking met k voor het aantal koeien en t voor het aantal tweepoters (waarbij we voor het rekengemak de gehandicapte kip zijn tweede pootje teruggeven), kun je de volgende twee vergelijkingen maken:
4k + 2t = 302
k + t = 125
t = 125 - k
4k + 2(125 - k) = 302
4k + 250 - 2k = 302
2k = 302 -250 = 52
k = 26
Zie ook de pagina Vergelijkingen.
TOTAALRESULTAAT:
Uitleg van de kleuren en symbolen:
© 2010 - Beter Rekenen is een initiatief van |

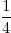 - 1
- 1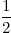 =
= 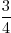
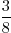
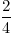 = 2
= 2