Antwoorden van 06-06-2025 (niveau 3F)
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 06-06-2025 zo ingevuld:
3(12 - 3 x 3) = ........
Eerst uitrekenen wat tussen de haakjes staat en dan 3 x 3 = 9
Zie ook de pagina Gemengde bewerkingen.
Zie ook de pagina Gemengde bewerkingen.
320 x ..... = 9,6
Van een rechthoekige driehoek is de schuine zijde 34 cm, een rechthoekszijde is 30 cm. De andere rechthoekszijde is ........ cm.
De stelling van Pythagoras zegt: a² + b² = c².
Oftewel: b² = c² - a².
b² = 34² - 30² = 1156 - 900 = 256 en dat is 16².
De zijden van deze driehoek hebben de verhouding 8:15:17 en dat is een mooie Pythagoras-combinatie.
Zie ook de pagina Pythagoras.
Oftewel: b² = c² - a².
b² = 34² - 30² = 1156 - 900 = 256 en dat is 16².
De zijden van deze driehoek hebben de verhouding 8:15:17 en dat is een mooie Pythagoras-combinatie.
Zie ook de pagina Pythagoras.
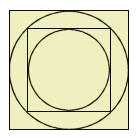
Een fabrikant van geschenkverpakkingen levert een pakket van een cilinder, een rechthoekige doos, nog een cilinder en nog een rechthoekige doos die achtereenvolgens precies in elkaar passen.
Zie de tekening (bovenaanzicht): de afgebeelde vlakken van de rechthoekige dozen zijn precies vierkant.
De kleinste verpakking is een cilinder met een diameter van 4 cm.
Daaromheen past precies een rechthoekige doos.
Daarna volgt er weer een cilinder.
En tot slot een rechthoekige doos.
Je mag de dikte van het karton verwaarlozen.
De oppervlakte van het grondvlak van de grootste verpakking is ........ cm².
(De stelling van Pythagoras, over rechthoekige driehoeken met rechthoekszijden a en b en schuine zijde c, zegt: a² + b² = c²)
(Een som van Harry Slieker.)
De afmetingen van het grondvlak van de vier verpakkingen zijn:
diameter kleine cilinder = 4 cm
zijde klein vierkant = 4 cm
diagonaal van klein vierkant is (4² + 4²) =
(4² + 4²) =  32 cm
32 cm
diameter grote cilinder = 32 cm
32 cm
zijde groot vierkant = 32 cm
32 cm
De oppervlakte van het grootste vierkant is 32 x
32 x  32 = 32 cm²
32 = 32 cm²
Zie ook de pagina Oppervlakte.
De afmetingen van het grondvlak van de vier verpakkingen zijn:
diameter kleine cilinder = 4 cm
zijde klein vierkant = 4 cm
diagonaal van klein vierkant is
 (4² + 4²) =
(4² + 4²) =  32 cm
32 cmdiameter grote cilinder =
 32 cm
32 cm zijde groot vierkant =
 32 cm
32 cmDe oppervlakte van het grootste vierkant is
 32 x
32 x  32 = 32 cm²
32 = 32 cm²Zie ook de pagina Oppervlakte.
TOTAALRESULTAAT:
Uitleg van de kleuren en symbolen:
Help | Contact | Instellingen |
Martin van Toll Producties
in samenwerking met
