Antwoorden van 10-06-2025 (niveau 3F)
10 JUN 
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 10-06-2025 zo ingevuld:
Verhoudingen:
1
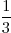: 12 is hetzelfde als 12 : ........ 
108 
andersJe hoeft dit niet te behandelen als twee deelsommen, maar als twee verhoudingen.
In de eerste verhouding is het linker getal 1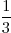 en in de tweede verhouding is het linker getal 12.
12 is 9 x 1.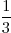
Als je het rechter getal uit de eerste verhouding ook vermenigvuldigt met 9, is de verhouding weer in balans: 9 x 12 = 108.
Zie ook de pagina Verhoudingen.
In de eerste verhouding is het linker getal 1
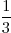en in de tweede verhouding is het linker getal 12.12 is 9 x 1
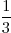.Als je het rechter getal uit de eerste verhouding ook vermenigvuldigt met 9, is de verhouding weer in balans: 9 x 12 = 108.
Zie ook de pagina Verhoudingen.
16 : 0,4 =
4646,440 Als je beide getallen 10 keer zo groot maakt, verandert dat niets aan de uitkomst, maar de som wordt wel makkelijker:
160 : 4 = 40
Zie ook de pagina Kommagetallen delen.
160 : 4 = 40
Zie ook de pagina Kommagetallen delen.
Een goudhandelaar legde ooit aan het einde van het jaar 1 gram goud apart voor zijn pensioen. Het volgende jaar 2 gram en het derde jaar 4, enzovoort.
Ieder volgend jaar legde hij twee keer zo veel goud apart als het jaar ervoor.
Aan het eind van het 20e jaar legde hij 524288 gram apart.
Na die 20 jaar had de man in totaal ........ gram goud bij elkaar gespaard.
(Vul een geheel getal in, zonder punten of spaties.)
1048575 anders(Een som van Wim de Graaf.)
Je hoeft niet alle twintig getallen onder elkaar zetten om op te tellen.
Kijk eens naar de paar eerste, nog overzichtelijke getallen:
Na de derde inleg is het 1 + 2 + 4 = 7 gram
Na de vierde inleg is het 1 + 2 + 4 + 8 = 15 gram.
De totaal gespaarde hoeveelheid is telkens het dubbele van de laatste inleg min 1 gram.
De 20e inleg is 524288 gram.
De totaal gespaarde hoeveelheid is het dubbele van 524288 min 1 gram.
2 x 524288 - 1 = 1048575
Na 20 jaar is de gespaarde hoeveelheid 1048575 gram.
Zie ook de pagina Gemengde bewerkingen.
Je hoeft niet alle twintig getallen onder elkaar zetten om op te tellen.
Kijk eens naar de paar eerste, nog overzichtelijke getallen:
Na de derde inleg is het 1 + 2 + 4 = 7 gram
Na de vierde inleg is het 1 + 2 + 4 + 8 = 15 gram.
De totaal gespaarde hoeveelheid is telkens het dubbele van de laatste inleg min 1 gram.
De 20e inleg is 524288 gram.
De totaal gespaarde hoeveelheid is het dubbele van 524288 min 1 gram.
2 x 524288 - 1 = 1048575
Na 20 jaar is de gespaarde hoeveelheid 1048575 gram.
Zie ook de pagina Gemengde bewerkingen.
TOTAALRESULTAAT:
71% goedUitleg van de kleuren en symbolen:
het juiste antwoord (door jou gekozen)
een fout antwoord (door jou gekozen)Help | Contact | Instellingen |
Martin van Toll Producties
in samenwerking met
