|
10603 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
 |
|
|
|
Dit is een muismat van Beter Rekenen:
Breuken, kommagetallen en procenten.
Een spiekbrief onder je muis bestellen?
Kies uit vier modellen.
Antwoorden van 08-08-2025 (niveau 3F)
08 AUG 
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 08-08-2025 zo ingevuld:
2 : 4 x 4 =
0,125
2 
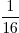
0,25Vermenigvuldigen en delen doe je in de volgorde zoals het er staat. In dit geval dus eerst delen, daarna vermenigvuldigen.
Zie ook de pagina Gemengde bewerkingen.
Zie ook de pagina Gemengde bewerkingen.
1,2 : .... = 2
0,6 60,81,67Als je deelt door een getal tussen 0 en 1, wordt de uitkomst groter. Het moet dus 0,6 of 0,8 zijn.
Je weet:
12 : 6 = 2
Nu is het een kwestie van komma's de juiste kant op schuiven:
1,2 : 6 = 0,2
1,2 : 0,6 = 2
Dat klopt, want
2 x 0,6 = 1,2
Zie ook de pagina Kommagetallen delen.
Je weet:
12 : 6 = 2
Nu is het een kwestie van komma's de juiste kant op schuiven:
1,2 : 6 = 0,2
1,2 : 0,6 = 2
Dat klopt, want
2 x 0,6 = 1,2
Zie ook de pagina Kommagetallen delen.
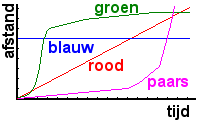
Met een van de lijnen in deze grafiek is de beweging van een auto getekend. Langs de horizontale as staat de tijd, langs de verticale as staat de afstand tussen de auto en de startstreep. De auto rijdt vanaf de startstreep langs een rechte weg langzaam tegen een lastige helling op. Als hij boven aan de helling komt, gaat hij sneller rijden.
Welke lijn hoort daarbij?
Langs de horizontale en verticale as van de grafiek zijn de stappen telkens even groot (lineaire schaalverdeling).
paars groenblauwroodDe paarse lijn loopt in het begin bijna horizontaal. De afstand tussen de startstreep en de auto groeit niet zo hard, maar na een tijdje groeit de afstand sneller, omdat de auto harder kan rijden.
Zie ook de pagina Diagrammen.
Zie ook de pagina Diagrammen.
Twee loodrecht op elkaar staande middellijnen verdelen een cirkel in vier gelijke delen. De verticale middellijn snijdt de cirkel bovenaan bij punt A, de andere snijdt de cirkel rechts bij punt B.
De lengte van de rechte verbindingslijn van A naar B is ........ procent van de lengte van de gebogen lijn tussen deze punten.
(Vul een geheel getal in. Indien nodig afronden.)
Tips:
Pythagoras zegt over een rechthoekige driehoek: de som van de kwadraten van de rechthoekszijden is gelijk aan het kwadraat van de schuine zijde.
De omtrek van een cirkel is 2 x pi x de straal.
Reken met pi = 3,14 en
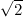= 1,414.De verhouding tussen de boog en de rechte lijn is altijd hetzelfde, ongeacht de afmeting. Reken daarom met een straal van 1 cm.
90 anders(Een som van Henk van Huffelen.)
De straal heeft lengte 1 cm.
De rechte lijn AB is de schuine zijde van een rechthoekige driehoek. De rechthoekszijden zijn beide 1 cm.
AB =
(1² + 1²) = (1 + 1) = 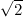= 1,414.
De gebogen lijn AB is een kwart van de cirkelomtrek. Dat is
1/4 x 2 x 3,14 =
1/2 x 3,14 = 1,57
1,414 is hoeveel procent van 1,57?
1% van 1,57 is 0,0157
1,414 : 0,0157 = 90,0637
Dat is afgerond 90.
Zie ook de pagina Omtrek.
De straal heeft lengte 1 cm.
De rechte lijn AB is de schuine zijde van een rechthoekige driehoek. De rechthoekszijden zijn beide 1 cm.
AB =
(1² + 1²) = (1 + 1) = 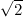= 1,414.De gebogen lijn AB is een kwart van de cirkelomtrek. Dat is
1/4 x 2 x 3,14 =
1/2 x 3,14 = 1,57
1,414 is hoeveel procent van 1,57?
1% van 1,57 is 0,0157
1,414 : 0,0157 = 90,0637
Dat is afgerond 90.
Zie ook de pagina Omtrek.
TOTAALRESULTAAT:
73% goedUitleg van de kleuren en symbolen:
het juiste antwoord (door jou gekozen)
een fout antwoord (door jou gekozen) 
Beter Spellen
Beter Rekenen
NU Beter Engels
NU Beter Duits
NU Beter Frans
NU Beter Spaans
Beter Bijbel
| © 2010 - Beter Rekenen is een initiatief van |