|
|
15485 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
|||
 |
|
|
|
Dit is een muismat van Beter Rekenen:
Het metriek stelsel: meters, liters en grammen.
Een spiekbrief onder je muis bestellen?
Kies uit vier modellen.
Antwoorden van 04-06-2025 (niveau 3F)
04 JUN 
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 04-06-2025 zo ingevuld:
In de computerwereld kom je weleens in aanraking met hexadecimale getallen. Deze getallen horen bij het zestientallig stelsel. Behalve de cijfers 0 t/m 9 zijn er ook nog de letters A t/m F. In onderstaand lijstje staan de hexadecimale getallen links van het isgelijkteken (de rode getallen).
Voor getallen vanaf 16 zijn twee tekens nodig: hexadecimaal getal 10=16, 11=17, enzovoort tot 1F=31. Dan komt hexadecimaal 20=32 en telt de reeks weer verder.
De decimale waarde van het hexadecimale getal 1D is ........ .
29 
andersDe 1 staat voor de zestientallen.
1 x 16 = 16
De D staat op de plaats van de eenheden. Hexadecimaal D betekent decimaal 13, zoals je in het lijstje ziet.
1D betekent 16 + 13 = 29
Zie ook de pagina Hexadecimale getallen.
1 x 16 = 16
De D staat op de plaats van de eenheden. Hexadecimaal D betekent decimaal 13, zoals je in het lijstje ziet.
1D betekent 16 + 13 = 29
Zie ook de pagina Hexadecimale getallen.
Vijf stukken, elk ter grootte van 4% van een hele kaas, zijn samen hetzelfde als ........ van deze kaas.
0,8 %
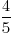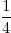deel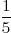
deel
deel 
625 gram - 0,4 hg + 950 mg = ........ mg
(Vul een geheel getal in, zonder punten, spaties of komma's.)
585950 andersEerst alles omzetten naar eenzelfde eenheid, bijvoorbeeld naar grammen:
1 hg = 100 gram
1 mg = 0,001 gram
625 - 40 + 0,95 = 585,95
585,95 gram = 585950 mg
Zie ook de pagina Gewicht.
1 hg = 100 gram
1 mg = 0,001 gram
625 - 40 + 0,95 = 585,95
585,95 gram = 585950 mg
Zie ook de pagina Gewicht.
Je schrijft een heel getal van 3 cijfers drie keer achter elkaar op. Je krijgt dan een getal van 9 cijfers.
Welk getal van 3 cijfers je ook neemt, het daaruit gevormde getal van 9 cijfers is altijd deelbaar door ........ .
(De uitkomst van de deling moet steeds een heel getal zijn.)
Als van de gegeven mogelijkheden meerdere antwoorden goed zijn, kies dan het grootste goede antwoord.
2963 (Een som van Jacques Schopman.)
Noem het getal abc en maak daarvan het getal abc abc abc.
De eerste 'abc' is 1.000.000 x abc.
Het middelste 'abc' is 1000 x abc.
En het laatste 'abc' is 1 x abc.
In totaal is 'abc.abc.abc' 1.001.001 keer abc.
1.001.001 is alleen deelbaar door 1 en 3.
Het juiste antwoord is 3.
Of:
Neem bijvoorbeeld 246.246.246.
246.246.246 : 246 = 1.001.001.
Altijd geldt: Als je een getal van 3 cijfers 3 keer achter elkaar zet, is dat getal van 9 cijfers 1.001.001 keer zo groot als het oorspronkelijke getal van 3 cijfers.
1.001.001 is alleen deelbaar door 1 en 3.
Het juiste antwoord is 3.
Zie ook de pagina Delen.
Noem het getal abc en maak daarvan het getal abc abc abc.
De eerste 'abc' is 1.000.000 x abc.
Het middelste 'abc' is 1000 x abc.
En het laatste 'abc' is 1 x abc.
In totaal is 'abc.abc.abc' 1.001.001 keer abc.
1.001.001 is alleen deelbaar door 1 en 3.
Het juiste antwoord is 3.
Of:
Neem bijvoorbeeld 246.246.246.
246.246.246 : 246 = 1.001.001.
Altijd geldt: Als je een getal van 3 cijfers 3 keer achter elkaar zet, is dat getal van 9 cijfers 1.001.001 keer zo groot als het oorspronkelijke getal van 3 cijfers.
1.001.001 is alleen deelbaar door 1 en 3.
Het juiste antwoord is 3.
Zie ook de pagina Delen.
TOTAALRESULTAAT:
66% goedUitleg van de kleuren en symbolen:
het juiste antwoord (door jou gekozen)
een fout antwoord (door jou gekozen)
Beter Spellen
Beter Rekenen
NU Beter Engels
NU Beter Duits
NU Beter Frans
NU Beter Spaans
Beter Bijbel
| © 2010 - Beter Rekenen is een initiatief van |